Очередь с приоритетом – это такая коллекция, которая поддерживает обязательно две следующие операции: вставка элемента с некоторым приоритетом (это может быть число или другой сравнимый объект) и извлечение элемента с наибольшим (или наименьшим приоритетом).
Очередь с приоритетом эффективно реализовать с помощью кучи. Двоичная куча – бинарное дерево, где значение в любой вершине не меньше (больше), чем значения её потомков, при этом заполнение уровней должно быть последовательным (без дырок и перескоков на следующий уровень, если текущий уровень не закончен). Работа с кучей осуществляется за время порядка O(log n). А построение кучи из массива – за O(n), где n – число элементов.
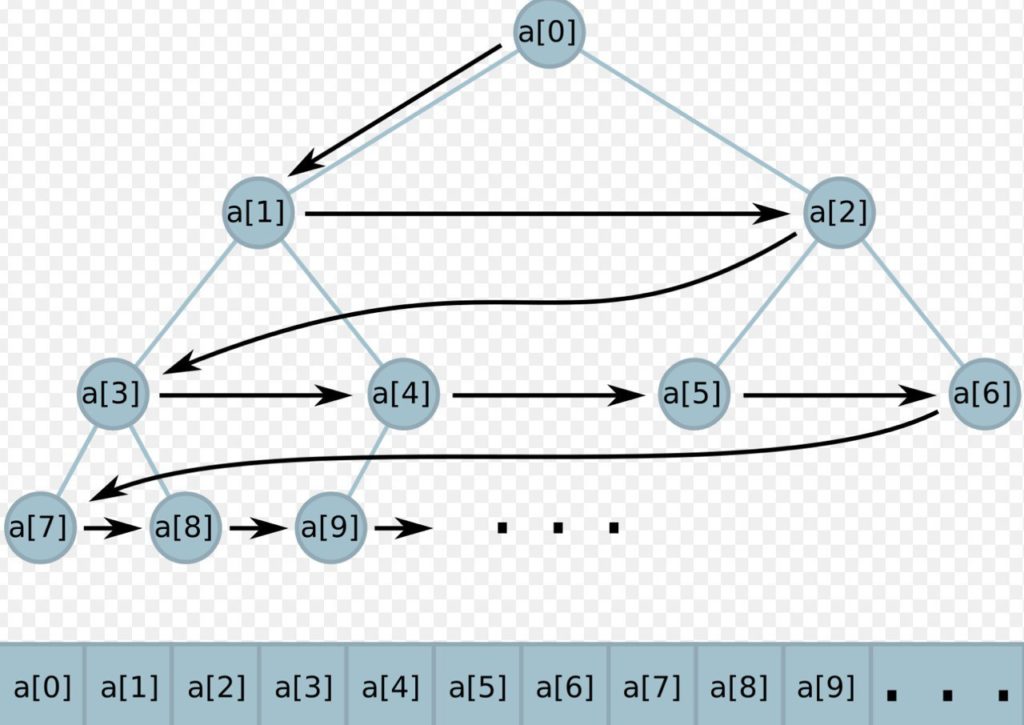
Кучу удобно хранить в массивах. Напомню, что списки (list) в Python – это и есть массивы переменной длины, а не связные списки (linked list), как в других языках. Поэтому доступ к элементу по индексу осуществляется за O(1). Пускай в корень дерева мы положим наименьший элемент, а корнем дерева будет нулевой элемент списка heap[0]. Его потомками будут элементы heap[1] и heap[2]. В общем виде потомками элемента heap[k] будут heap[2*k+1] и heap[2*k+2]. Такая индексация позволяет хранить в массиве двоичное дерево компактно и удобно получать доступ к его элементам. По условиям кучи должны соблюдаться условия heap[k] <= heap[2*k+1] и heap[k] <= heap[2*k+2].
В Python есть модуль heapq, который предоставляет процедурный интерфейс по работе с двоичными кучами, причем его функции принимают в качестве кучи именно обычные объекты типа list.
Создать кучу можно двумя способами:
- начать с пустого списка [] и заполнить его методом heappush
- взять существующий список и превратить его в кучу на месте (in-place) функцией heapify. heapify не возвращает новый список, а модифицирует переданный:
import heapq x = [3, 1, 4, 2, 5] heapq.heapify(x) >>> x [1, 2, 4, 3, 5]
Основные функции:
▶ heappush(heap, item) – добавляет в кучу элемент item.
▶ heappop(heap) — возвращает наименьший элемент и удаляет его из кучи. Если не надо удалять, то просто heap[0].
▶ heappushpop(heap, item) – добавляет в кучу item, а после возвращает наименьший элемент (работает немного быстрее, чем в две операции).
▶ heapreplace(heap, item) – возвращает наименьший элемент, а потом уже добавляет новый item (работает немного быстрее, чем в две операции).
ℹ️ Помните! Отсортированный список является кучей – это лекго проверить по условиям. Поэтому если ваш массив заранее отсортирован, то не надо вызывать heapq.heapify.
ℹ️ Но не любая куча – отсортированный список. Построение из массива – кучи, а из кучи – отсортированного массива – это сортировка кучей: мы наполняем последовательно кучу, а потом по порядку извлекаем наименьшие элементы, пока куча не истощится:
def heapsort(iterable):
h = []
for value in iterable:
heapq.heappush(h, value)
return [heapq.heappop(h) for i in range(len(h))]
>>> heapsort([1, 3, 5, 7, 9, 2, 4, 6, 8, 0])
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
В примерах выше, мы пользовались числами, как элементами кучи, потому что числа легко сравнимы. В реальной жизни мы оперируем произвольными объектами с их приоритетами. Для перехода от кучи к очереди с приоритетами можно использовать следующий трюк: использовать как элементы кортежи вида (приоритет, объект) или (приоритет, идентификатор, объект), если объекты несравнимы. Приоритет – число (например: важность задачи или время запуска какого-либо процесса). Идентификатором может служить порядковый номер.
q = [] heapq.heappush(q, (-priotiry, ident, obj)) ident += 1
Куча возвращает минимальный элемент (heappop), а кортежи сравниваются поэлементно слева направо. Сначала идет -priotiry. Знак минус, чтобы сначала возвращался не минимальный приоритет, а максимальный. Если приоритеты равны, то будет возвращен элемент с наименьшим идентификатором ident, т.е. тот, что был добавлен раньше всех для данного значения приоритета.
Полный пример кода очереди с приоритетами доступен по ссылке.
🧙 Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈