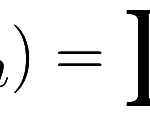В Python есть встроенный тип данных complex, который моделируют комплексные числа. По-моему, теория комплексных чисел – настоящий прорыв в математике, оказавший колоссальное влияние на современную физику. Неудивительно, что комплексные числа оказались в стандартной библиотеке такого языка, как Python.

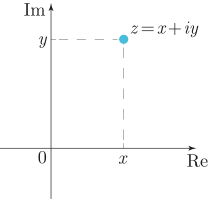
Ко́мпле́ксные чи́сла — числа вида a + bi, где a, b — вещественные числа, i — мнимая единица, то есть число, для которого выполняется равенство: i2 = -1.
Цель этой статьи – рассказать про комплексные числа с точки зрения программирования на Python, если вам хочется узнать математическую теорию или просто освежить воспоминания о комплексных числах, то смело переходите по ссылке: Комплексные числа (откроется в новом окне), а потом возвращайтесь сюда.
В Python комплексное число состоит из пары чисел с плавающей запятой, которые отвечают за реальную и мнимые части. В исходнике на Си – это структура из пары чисел типа double. (Вы же помните, что float в Python это числа двойной точности?):
typedef struct {
double real;
double imag;
} Py_complex;
✅ Давайте посмотрим, какими способами мы можем задать комплексное число. Во-первых, с помощью встроенной функции complex(real[, imag]):
>>> complex() # нуль! (комплексный)
0j
>>> complex(1) # из обычного числа int или float (мнимая часть будет 0)
(1+0j)
>>> complex(2, 3) # из пары чисел (реальная и мнимая части)
(2+3j)
>>> complex('2+3j') # из строки (без пробелов)!
(2+3j)
❌ Когда создаете комплексное число из строки, то в ней не должно быть пробелов, иначе будет ошибка ValueError!
✅ Во-вторых, что очень круто, комплексное число можно задать особым синтаксисом в форме a+bj. Примеры:
>>> 8+5j (8+5j) >>> -1-1j (-1-1j) >>> 0j 0j >>> -4.4e+5 + 1.5e+6j (-440000+1500000j)
❌ Но! Нельзя задавать их так:
>>> 1+j Traceback (most recent call last): File "<stdin>", line 1, in <module> NameError: name 'j' is not defined >>> a = 5 >>> 2 + aj Traceback (most recent call last): File "<stdin>", line 1, in <module> NameError: name 'aj' is not defined
В первом случае надо писать 1j, вместо j, потому что j – это может быть название какой-то иной переменной, ведь имя j не зарезервировано под мнимую единицу. Чтобы задать мнимое число, обязательно требуется перед j ставить цифры.
Во втором случае, мы желаем задать мнимую часть через переменную, но Python думает, что у нас должна быть переменная с именем aj, которой нет. Правильно писать в таком случае a*1j.
✅ Правильные варианты:
>>> 1+1j (1+1j) >>> a = 5 >>> 2 + a * 1j (2+5j)
Кстати, буква j может быть и заглавной J.
Какие свойства есть у типа complex?
Можно извлекать из комплексного числа его мнимую (imag) и реальную (real) части – это обычные float:
>>> z = -3+7j >>> z.real, z.imag (-3.0, 7.0) >>> z == z.real + z.imag * 1j True
Комплексно-сопряженное число – то же самое, только с другим знаком у мнимой части:
>>> z.conjugate() (-3-7j) >>> (4-1j).conjugate() (4+1j)
Модуль комплексного числа – фактически длина вектора на комплексной плоскости – вычисляется обычной функцией abs:
>>> abs(4+3j) 5.0
Операции
✅ К комплексным числам применимы обычные арифметический операторы, такие как +, -, *, /.
Как вы догадались из формы синтаксиса 1+2j, можно без проблем складывать комплексные числа с обычными вещественными float или целыми int. Т.е. полное комплексное число в этой форме представляется суммой действительного числа и чисто мнимого. Аналогично, умножение комплексного числа на вещественное просто масштабирует пропорционально его компоненты на это число.
Пару комплексных чисел можно складывать и вычитать. Это просто, они работают подобно двумерным векторам на плоскости. Комплексные числа можно умножать и делить. Тут математика несколько сложнее, не буду повторять ее, читайте вики. А примеры кода вот:
>>> z1 = 3 + 4j >>> z2 = 5 - 2j >>> z1 + z2 (8+2j) >>> z1 - z2 (-2+6j) >>> z1 * z2 (23+14j) >>> z1 / z2 (0.24137931034482757+0.896551724137931j)
Не забывайте ставить скобки:
>>> 1+2j * 5-4j (1+6j) >>> (1+2j) * (5-4j) (13+6j)
❌ Целочисленные деления, взятие остатка и подобное не применимы к комплексным числам.
✅ Комплексные числа можно сравнивать на равенство и неравенство.
>>> 1+2j == 2j+1 True >>> 3 + 4j != 2 - 2j True
❌ Но нельзя к ним применять знаки больше, меньше.
>>> 1j > 2j Traceback (most recent call last): File "<stdin>", line 1, in <module> TypeError: '>' not supported between instances of 'complex' and 'complex'
✅ Можно возводить одно комплексное число в степень другого следующими способами*:
>>> z1 ** z2 (3046.7438186304985+19732.04597993193j) >>> pow(z1, z2) (3046.7438186304985+19732.04597993193j)
Комплексный 0 в степени комплексного 0 даст… барабанная дробь… единицу:
>>> 0j ** 0j (1+0j)
*) О многозначности замолвлено будет ниже, математики приберегите свои помидоры, пока не дочитаете до конца.
cmath
Модуль, который отвечает за стандартные функции над комплексными числами называется cmath (документация на английском). Обычный math не умеет извлекать корень из минус единицы, а cmath – запросто:
>>> import math, cmath >>> math.sqrt(-1) Traceback (most recent call last): File "<stdin>", line 1, in <module> ValueError: math domain error >>> cmath.sqrt(-1) 1j
Рассмотрим основные функции из cmath:
cmath.phase(x) – фаза (или у нас она более известна, как аргумент Arg z) – эквивалент math.atan2(x.imag, x.real) – иными словами, это угол поворота φ вектора на комплексной плоскости. Результат лежит в промежутке [-π, π]. При этом разрез на комплексной области (т. е. луч, через который результат функции разрывается и перепрыгивает) выбирается вдоль отрицательной части реальной оси).
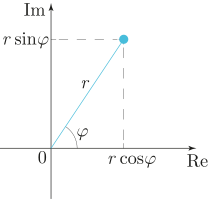
>>> phase(complex(-1.0, 0.0)) 3.141592653589793 >>> phase(complex(-1.0, -0.0)) # минус ноль! подходим с другой стороны к точке разреза -3.141592653589793
За модуль отвечает обычная abs (без cmath).
cmath.polar(x) – перевод комплексного числа в полярные координаты (кортеж из двух float): (abs(x), cmath.phase(x)).
cmath.rect(r, phi) – наоборот выдает комплексное число по его полярным координатам – эквивалент: r * (math.cos(phi) + math.sin(phi)*1j).
cmath.sqrt(x) – корень квадратный из комплексного числа.
>>> cmath.sqrt(1j) (0.7071067811865476+0.7071067811865475j)
Те, кто разбирается в математике сразу заметят, что многие функции от комплексной переменной – многозначны. (Видео о многозначных функциях) В частности у корня квадратного из комплексного числа всегда ровно два ответа. Но! Python всегда возвращает ровно одно значение. Он берет всегда «главную ветвь», а всякие вращения на 2πk/n остаются на совести программиста. Вот теория, как брать корень из комплексного числа. Я тщетно пытался нагуглить функцию, возвращающую множество значений корня n-й степени, и в итоге написал свою:
import cmath
def roots(z: complex, n):
assert isinstance(n, int) and n > 1
r, phi = cmath.polar(z)
r **= 1 / n
for k in range(n):
yield cmath.rect(r, (phi + 2 * cmath.pi * k) / n)
z1, z2 = roots(1j, 2)
print(z1, z2)
print(cmath.isclose(z1 * z1, 1j))
print(cmath.isclose(z2 * z2, 1j))
# (0.7071067811865476+0.7071067811865475j) (-0.7071067811865477-0.7071067811865475j)
# True
# True
Функция cmath.isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0) проверяет близки ли два комплексных числа между собой с некоторой точностью (относительной или абсолютной). Так как complex строится на базе чисел с плавающей точкой, то из-за ошибок округления редко можно получить точное равенство, приходится проверять близость. Код эквивалентен: abs(a-b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol). Числа NaN не близки ни к кому, включая самих себя. А inf и -inf близки только каждое само к себе.
cmath.exp(x),cmath.log(x[, base]), cmath.log10(x), cmath.acos(x), cmath.asin(x), cmath.atan(x), cmath.cos(x), cmath.sin(x), cmath.tan(x), cmath.acosh(x), cmath.asinh(x), cmath.atanh(x), cmath.cosh(x), cmath.sinh(x), cmath.tanh(x) – обычный набор функций, только для комплексных чисел. Каждая из функций возвращает один результат. Думаю, если вам действительно нужны в работе комплексные функции, значит вы и так знаете, как достать все значения функций.
Множество Мандельброта
Даже если вы не математик или физик, комплексные числа могут поразвлечь и вас. Решил, что прикладной пример о комплексных числах должен быть впечатляющим. Мы нарисуем множество Мандельброта – пожалуй самый знаменитый фрактал.
Мно́жество Мандельбро́та — это множество таких точек c на комплексной плоскости, для которых рекуррентное соотношение задаёт ограниченную последовательность.
Иными словами мы берем каждую точку с = x + yj на выбранном участке комплексной плоскости и возводим в квадрат, потом снова прибавляем c, опять возводим в квадрат и так несколько раз. Смотрим, улетает ли результат в бесконечность. Если не улетает, значит точка принадлежит множеству, красим ее в черный, а если улетает, то красим в белый.
Нам понадобятся библиотеки для работы с изображениями и для полосы прогресса:
pip install pillow tqdm
Пишем код:
from PIL import Image
from tqdm import tqdm
W, H = 1024, 768 # размеры картинки
ITER = 100 # максимальное число итераций, чтобы убедиться расходится или нет формула в данной точке
LIMIT = 2.0 # предельное значение, выше которого уже наверняка расходится
img = Image.new('RGB', (W, H))
for px in tqdm(range(W)):
for py in range(H):
# преобразование координат
x = px / W * 3 - 2 # x = -2..1
y = py / H * 2 - 1 # y = -1..1
color = (0, 0, 0) # черный
c = x + 1j * y # смещение из координат
z = 0j # начальная точка
for n in range(ITER):
z = z ** 2 + c
if abs(z) > LIMIT: # разошлось
color = (255, 255, 255) # белый цвет
break
img.putpixel((px, py), color)
img.save('mand0.png') # сохраним
img.show() # покажем
Результат:

Добавим цвета. Будем считать, сколько итераций прошел цикл перед тем, как последовательность разошлась и мы вышли. Каждому числу шагов зададим цвет на палитре. Цвета плавно меняются вдоль палитры.
from PIL import Image
from tqdm import tqdm
import math
W, H = 1024, 768 # размеры картинки
ITER = 1000 # максимальное число итераций, чтобы убедиться расходися или нет формула в данной точке
LIMIT = 2.0 # предельное значение, выше которого уже расходится
img = Image.new('RGB', (W, H))
# создадим палитру от числа итераций
palette = [
(
int(255 * math.sin(i / 50.0 + 1.0) ** 2),
int(255 * math.sin(i / 50.0 + 0.5) ** 2),
int(255 * math.sin(i / 50.0 + 1.7) ** 2)
) for i in range(ITER - 1)
]
palette.append((0, 0, 0)) # последняя итерация - значит мы внутри - черный
for px in tqdm(range(W)):
for py in range(H):
# преобразование координат
x = px / W * 3 - 2 # x = -2..1
y = py / H * 2 - 1 # y = -1..1
c = x + 1j * y # смещение из координат
z = 0j # начальная точка
for n in range(ITER):
z = z ** 2 + c
if abs(z) > LIMIT: # разошлось
break
img.putpixel((px, py), palette[n])
img.save('mand1.png') # сохраним
img.show() # покажем
Вот итог:

Вот такая красота получается из простейшей формулы!
Можно пойти дальше и создать GIF анимацию, где мы постепенно приближаемся к деталям фрактала. Перед этим оптимизируем немного код. abs извлекает квадратный корень, что не обязательно. Лучше сделать так, для улучшения производительности:
if (z * z.conjugate()).real > 4.0: # вместо abs(z) > 2.0!
break
От кадра к кадру будем менять область отображения. Генератор фрактала для заданной области описан функцией:
def mandelbrot(w, h, palette, x1=-2, y1=-1, x2=1, y2=1):
img = Image.new('RGB', (w, h))
dx = x2 - x1
dy = y2 - y1
iters = len(palette)
n = 0
for px in range(w):
for py in range(h):
# преобразование координат
x = px / w * dx + x1
y = py / h * dy + y1
c = x + 1j * y # смещение из координат
z = 0j # начальная точка
for n in range(iters):
z = z ** 2 + c
if (z * z.conjugate()).real > 4.0: # разошлось
break
img.putpixel((px, py), palette[n])
return img
Остаетя задать закон движения камеры и сохранить пачку кадров в GIF.
x, y, r = 0, 0, 5 # от
x_tar, y_tar, r_tar = -0.74529, 0.113075, 1.5e-6 # до
frames = []
for _ in tqdm(range(FRAMES)):
frames.append(mandelbrot(W, H, palette, x - r, y - r, x + r, y + r))
x += (x_tar - x) * 0.1
y += (y_tar - y) * 0.1
r += (r_tar - r) * 0.1
frames[0].save('mandel.gif', save_all=True, append_images=frames[1:], duration=60, loop=0)
Полный код генератора анимации здесь.

Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈