Хочу пописать немного про математику, статистику, анализ данных и машинное обучение. Но для этого надо начать с небольшой базы по представлению вещественных чисел в Python.
Кто-то, вероятно, слышал о проблеме 0.1 + 0.1 + 0.1 == 0.3. Вкратце, вбейте в интерпретаторе Python:
>>> 0.1 + 0.1 + 0.1 == 0.3 False
Здравый смысл подсказывает нам, что здесь что-то не так, должно же равняться! Новичков это вообще может вбить в ступор. Программисты поопытнее могут объяснить это ошибками округления float-чисел. Давайте же разберемся, что на самом деле там происходит.
Экспоненциальное представление чисел
Стандарт IEEE-754 регулирует, как должны представляться вещественные числа в железе (процессорах, сопроцессорах и так далее) и программном обеспечении. Так много вариантов представлений, но на практике почти везде сейчас используются числа с плавающей точкой одинарной или двойной точности, причем оба варианта с основанием 2, это важно.
Плавающая точка
Почему точка плавающая? Потому что числе представлены внутри компьютера экспоненциальном формате:
Число = ±мантисса * основаниеэкпонента
Меняя экспоненту можно двигать положение точки в любую сторону. Например, если основание было бы 10, то числа 1,2345678; 1 234 567,8; 0,000012345678; 12 345 678 000 000 000 отличались бы только экспонентой.
float в Python
float – встроенные тип в Python (CPython) и представляет собой число с плавающей точкой двойной точности, независимо от системы и версии.
float в Python – это double из C, C++, C# или Java и имеет 64 бита (8 байт) для хранения данных о числе.
Примечание: сторонними библиотеками можно получить и другие типы, а еще есть Decimal.
В эти 64 бита упакованы как 11 бит на экспоненту и 52 бита на мантиссу (+ 1 бит на знак, итого 53). Вот так:
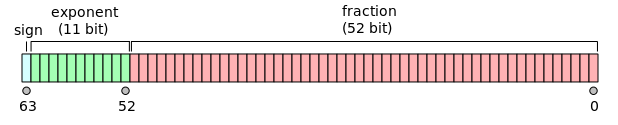
Думаете, любое реальное число можно представить, используя эти 64 бита? Конечно, нет. Простая комбинаторика скажет, что у нас может быть не более 264 разных чисел (64 позиции по 2 варианта), а на деле их и того меньше. Диапазон чисел, представимых таким форматом составляет: ±1.7*10-308 до 1.7*10+308. То есть от очень малых по модулю чисел, до очень больших. Допустимые числа на числовой прямой распределены неравномерно: гуще в районе нуля и реже в районе огромных чисел.
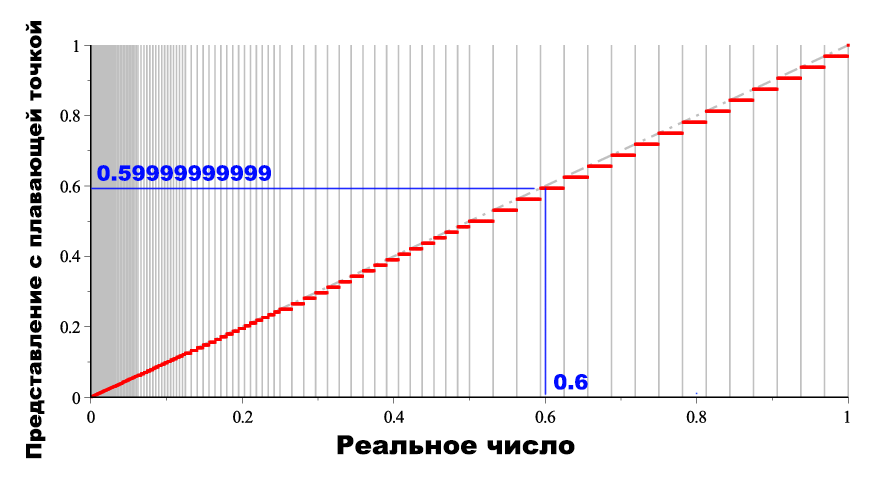
Источник ошибок
Откуда же берутся ошибки?
Дело в том, что числа 0.1 – нет! Действительно, нет способа представить это немудреное число в формате с плавающей точкой с основанием 2!
0.1 – это просто текст, для которого Python должен подобрать максимально близкое представление в памяти компьютера. Можно найти число поменьше или побольше, но точно 0.1 – не получится. Все дело в основании 2 – именно двойка фигурирует под степенью. Надо подобрать такие J и N, чтобы получить число максимально близкое к 0.1:
0.1 = 1 / 10 ≈ J / (2**N) или J ≈ 2**N / 10
При этом в J должно быть ровно 53 бита. Наиболее подходящие N для такого случая равняется 56.
>>> 2**52 <= 2**56 // 10 < 2**53 True >>> divmod(2**56, 10) (7205759403792793, 6)
Остаток от деления – 6 чуть больше половины делителя (10), поэтому наилучшее приближение будет, если мы округлим частное вверх, то есть добавим к 7205759403792793 + 1 = 7205759403792794. Таким образом, это будет ближайшее к 0.1 число, возможное в представлении float. Доказательство проверкой:
>>> 7205759403792794 / 2 ** 56 == 0.1 True
Оно чуть больше, чем реальное 0.1. Если бы мы не прибавили единицу, то получилось бы число чуть меньшее, чем 0.1, но никакое сочетание J и N не даст нам ровно 0.1 ни в едином случае!
>>> format(7205759403792793 / 2 ** 56, '.56f') '0.09999999999999999167332731531132594682276248931884765625' >>> format(7205759403792794 / 2 ** 56, '.56f') '0.10000000000000000555111512312578270211815834045410156250'
Это два соседних числа. Между ними не может быть других промежуточных чисел, в том числе и самого 0.1! Множество чисел, представимых числом с плавающей точкой дискретно и конечно, в нем нет всех возможных чисел.
Теперь понятно, что 0.1 и 0.3 аппроксимируются к каким-то ближайшим представлениям в экспоненциальной форме в памяти компьютера. Поэтому и возникает эта разница:
>>> format(0.1 + 0.1 + 0.1 - 0.3, '.56f') '0.00000000000000005551115123125782702118158340454101562500'
Она мала, но она есть! Именно поэтому никогда не советуют точно сравнивать числа типа float, даже если для вас они равны, их представления могут отличаться, если числа получены разным путем. Могут отличаться, а могут и совпадать! Так что это может сыграть злую шутку.
>>> 0.15 + 0.15 == 0.3 True >>> 0.1 + 0.15 + 0.05 == 0.1 + 0.1 + 0.1 False >>> 0.1 + 0.15 + 0.05 0.3 >>> 0.1 + 0.1 + 0.1 0.30000000000000004
Там есть функция, которая делает более аккуратное сложение IEEE-754 чисел, но она тоже работает не идеально. На примере из документации – отлично и проваливается на нашем пресловутом триплете из 0.1:
>>> sum([0.1] * 10) == 1.0 False >>> math.fsum([0.1] * 10) == 1.0 True # не тут то было! >>> math.fsum([0.1] * 3) == 0.3 False
Поверьте, это не единственная особенность такого представления чисел. Я обязательно расскажу больше. Будьте на связи!
Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈