Эта тема не очень освещена на русском языке, но является весьма важной по паре причин: бродкастинг упрощает жизнь, и порой он же ее усложняет. Давайте разберемся что это, и как оно работает?
Бродкастинг (broadcasting) – автоматическое расширение размерности (ndim) и размеров (shape) массивов, при совершении операций (сложение, умножение и подобные) над массивами с разными размерами или размерностями, при условии, что они совместимы с правилами бродкастинга.
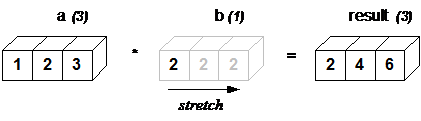
Очень животрепещущий пример из жизни, где вы используете бродскастинг и даже об этом не думаете: совершение операций между вектором и скаляром. Что значит умножить вектор на число? Вероятно, каждый скажет, что это значит, что нужно домножить каждый компонент этого вектора на это число. Иными словами, можно копировать число столько раз, сколько у нас компонент в векторе, получив из числа вектор той же размерности, а потом поэлементно умножить эти вектора:
>>> y = np.array([2] * 3) >>> y array([2, 2, 2]) >>> x * y array([2, 4, 6]) >>> x = np.array([1, 2, 3]) >>> x * 2 array([2, 4, 6])
NumPy не заставляет нас вручную превращать скаляр (2) в вектор [2, 2, 2], он сам добавляет размерность и клонирует содержимое нужно число раз, а потом уже производит поэлементное умножение.
Я скажу больше, что бродкастинг в данном случае не только дает удобство, но и прирост производительности и экономию памяти, потому что NumPy совершает эти операции эффективно в своем оптимизированном Си-коде и не создает лишних копий данных.
Бродкастинг работает и в более сложных ситуациях по четким правилам.
Правила бродкастинга
Буду сразу объяснять на примере. Есть два массива, которые мы желаем сложить:
>>> a = np.ones((8, 1, 6, 1)) >>> b = np.ones((7, 1, 5)) >>> a.shape (8, 1, 6, 1) >>> b.shape (7, 1, 5) # (a + b) = ?
Сначала размеры (shape) массивов выстраивается друг над другом, выравнивая по правому краю. Напомню, что справа у нас самая «глубокая» размерность.
A (4d массив): 8 x 1 x 6 x 1 B (3d массив): 7 x 1 x 5
Затем NumPy идет справа налево, поэлементно сравнивая каждый размер операндов. Два размера считаются совместимыми, если они равны или один из них равен единице (1). Если два размера несовместимы, бродкастинг не пройдет, возникнет ошибка. ValueError: operands could not be broadcast together with shapes
Если слева не хватает размерности, то она автоматически расширяется единицей, это значит, что мы как будто бы оборачиваем массив в еще одни квадратные скобки. В нашем примере, у B не хватает одной размерности, так как он трехмерный вектор, а мы превратим его в четырехмерный.
A (4d массив): 8 x 1 x 6 x 1 B (3d массив): 7 x 1 x 5 B' (4d массив): 1 x 7 x 1 x 5 B' = [ B ]
Мы видим, что в примере два массива полностью совместимы для бродкастинга – (8 над 1, 1 над 7, 6 над 1, 1 над 5): в каждом из столбиков есть единичка.
Теперь происходит самое интересное – там, где размеры это единицы происходит «копирование» каждого из таких измерений столько раз, чтобы размеры по этому измерению стали равны.
A (4d массив): 8 x 1 x 6 x 1 B (3d массив): 7 x 1 x 5 Результат (4d массив): 8 x 7 x 6 x 5
Т. е. у A на глубоком уровне по одному числу, а у B – по 5 штук. Примерно так:
A = [ [ [ [123], ... ] ], ... ] B = [ [ [456, 456, 456, 456, 456] ], ... ] A' = [ [ [ [123, 123, 123, 123, 123], ... ] ], ... ]
Значит внутренний подмассив [123] у A тоже раскопируется в 5 значений [123, 123, 123, 123] и, таким образом, станет совместим с внутренним подмассивом B, где уже было 5 чисел.
Как только все размерности выровнены путем «копирования», то можно делать любую операцию поэлементно. Форма результата будет равна форме операндов. В итоге:
>>> (a + b).shape (8, 7, 6, 5)
Еще примеры
Примеры привожу по следам документации. Такой код:
import numpy as np
a = np.array([[0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]])
b = np.array([1, 2, 3])
print(a + b)
# [[ 1 2 3]
# [11 12 13]
# [21 22 23]
# [31 32 33]]
Работает по следующей схеме:
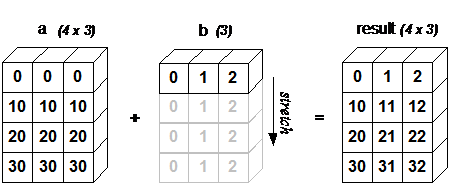
Еще больше примеров, как получается финальный размер после операции:
Картинка (3d массив) 256 x 256 x 3 Масштаб (1d массив) 3 Результат (3d массив) 256 x 256 x 3 A (2d array): 5 x 4 B (1d array): 1 Result (2d array): 5 x 4 A (2d array): 5 x 4 B (1d array): 4 Result (2d array): 5 x 4 A (3d array): 15 x 3 x 5 B (3d array): 15 x 1 x 5 Result (3d array): 15 x 3 x 5 A (3d array): 15 x 3 x 5 B (2d array): 3 x 5 Result (3d array): 15 x 3 x 5 A (3d array): 15 x 3 x 5 B (2d array): 3 x 1 Result (3d array): 15 x 3 x 5
Примеры несовместимости
А вот примеры несовместимости:
A (1d array): 3 B (1d array): 4 # не совпадают 3 и 4 (и ни одна из них не 1) A (2d array): 2 x 1 B (3d array): 8 x 4 x 3 # второй столбик справа не совпадает (2 и 4)
Такой код на практике даст ошибку:
import numpy as np
a = np.array([[0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]])
b = np.array([0, 1, 2, 3])
print(a + b)
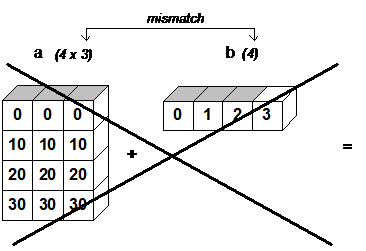
# ValueError: operands could not be broadcast together with shapes (4,3) (4,)
Потому что тут бродкастинг не работает, так как нарушены его правила:
Опасность бродкастинга
Бродкастинг удобен, но может и навредить, потому что он не дает предупреждений, что массивы разного размера. Иными словами, можно умножить синий цвет на число крокодилов, и если повезло с размерностью крокодилов и цвета, то вы еще долго будете искать ошибку.
Я пока не нашел опции запретить бродкастинг в NumPy, а ответы со Stackoverflow вроде [1], [2] оказались НЕРАБОЧИМИ. Как всегда, будьте осторожны!
Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈