Комбинаторика — это раздел математики, в котором изучают, сколько комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов. Короче, это все о сочетаниях, перестановках, числе способов и тому подобному.
Почему важна комбинаторика? Нет, не только лишь для решения олимпиадных задач, но также комбинаторика – один из столпов теории вероятностей, которая в свою очередь служит фундаментом для машинного обучения – одно из мощнейших трендов в ПО начале 21-го века!
В встроенном в Python модуле itertools существует ряд комбинаторных функций. Это:
product()– прямое (Декартово) произведение одного или нескольких итераторов.permutations()– перестановки и размещения элементов множества.combinations()– уникальные комбинации из элементов множества.combinations_with_replacement()– комбинации с замещением (повторами, возвратами).
О каждой из них расскажу подробно. Для начала импортируем все нужные функции из модуля:
from itertools import *
Прямое произведение
Прямое, или декартово произведение двух множеств — множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств. Проще говоря мы берем из первого множества один элемент, а потом из второго выбираем элемент и составляем их в кортеж. Так вот все способы выбрать так элементы – составят декартово произведение. Пример:
>>> A = [1, 2, 3] >>> B = "123" >>> print(*product(A, B)) (1, 'a') (1, 'b') (1, 'c') (2, 'a') (2, 'b') (2, 'c') (3, 'a') (3, 'b') (3, 'c')
Примечания. Во-первых, заметьте, что элементы следуют в строгом лексографическом порядке: сначала берется нулевой элемент из первой последовательности и сочетается с каждым по очереди из второй последовательности. Во-вторых, аргументами функции могут быть любые итерируемые объекты конечной длины. Я взял для примера список и строку, причем строка автоматически разбивается на символы.
В коде произведение множеств эквивалентно вложенным циклам:
>>> print(*[(a, b) for a in A for b in B]) (1, '1') (1, '2') (1, '3') (2, '1') (2, '2') (2, '3') (3, '1') (3, '2') (3, '3')
Результат такой же, но рекомендую использовать именно библиотечную функцию, так как ее реализация, наверняка, будет лучше.
Вы можете передать в функцию больше последовательностей:
>>> print(*product([1, 2, 3])) (1,) (2,) (3,) >>> print(*product([1, 2, 3], [10, 20, 30])) (1, 10) (1, 20) (1, 30) (2, 10) (2, 20) (2, 30) (3, 10) (3, 20) (3, 30) >>> print(*product([1, 2, 3], [10, 20, 30], [100, 200, 300])) (1, 10, 100) (1, 10, 200) (1, 10, 300) (1, 20, 100) (1, 20, 200) (1, 20, 300) (1, 30, 100) (1, 30, 200) (1, 30, 300) (2, 10, 100) (2, 10, 200) (2, 10, 300) (2, 20, 100) (2, 20, 200) (2, 20, 300) (2, 30, 100) (2, 30, 200) (2, 30, 300) (3, 10, 100) (3, 10, 200) (3, 10, 300) (3, 20, 100) (3, 20, 200) (3, 20, 300) (3, 30, 100) (3, 30, 200) (3, 30, 300)
Каждый выходной элемент будет кортежем (даже в случае, если в нем только один элемент!). Также обратите внимание на то, что функция product (как и все остальные из сегодняшнего набора) возвращает не список, а особый ленивый объект. Чтобы получить все элементы, нужно преобразовать его в список функцией list:
>>> product([1, 2, 3], 'abc') <itertools.product object at 0x101aef8c0> >>> list(product([1, 2, 3], 'abc')) [(1, 'a'), (1, 'b'), (1, 'c'), (2, 'a'), (2, 'b'), (2, 'c'), (3, 'a'), (3, 'b'), (3, 'c')]
Количество элементов на выходе будет произведением длин всех последовательностей на входе:
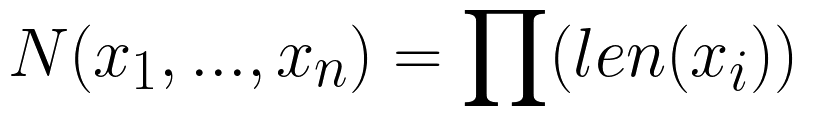
В функцию product можно передать именованный параметр repeat, который указывает сколько раз повторять цепочку вложенных циклов (по умолчанию один раз). Если repeat >= 2, то это называют декартовой степенью. То есть множество умножается на себя несколько раз. Так при repeat=2 эквивалентным кодом будет:
>>> [(a, b, a1, b1) for a in A for b in B for a1 in A for b1 in B] == list(product(A, B, repeat=2)) True
В таком случае количество элементов в результате будет вычисляться по схожей формуле с учетом того, что каждый множитель будет в степени repeat:
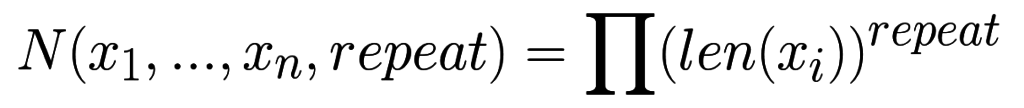
Перестановки
Функция permutations возвращает последовательные перестановки элементов входного множества. Первый элемент – будет исходным множеством. Второй – результат перестановки какой-то пары элементов и так далее, пока не будут перебраны все уникальные комбинации. Уникальность здесь рассматривается по позициям элементов в исходной последовательности, а не по и их значению, то есть элементы между собой алгоритмом не сравниваются. Важны только их индексы.
Число объектов остается неизменными, меняется только их порядок.
>>> print(*permutations("ABC"))
('A', 'B', 'C') ('A', 'C', 'B') ('B', 'A', 'C') ('B', 'C', 'A') ('C', 'A', 'B') ('C', 'B', 'A')
Второй параметр r отвечает за количество элементов в перестановках. По умолчанию будут выданы полные перестановки (длиной, равной длине n исходной последовательности), никакие элементы исходного множества не будут выброшены, а просто переставлены местами. Если задать 0 <= r <= n, в каждой выборке будет содержаться по r элементов. Иными словами из n входных элементов будем выбирать r объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по r.
Например размещения для двух элементов из коллекции из трех элементов:
>>> print(*permutations("ABC", 2))
('A', 'B') ('A', 'C') ('B', 'A') ('B', 'C') ('C', 'A') ('C', 'B')
# 2 из 4
>>> print(*permutations([1, 2, 3, 4], 2))
(1, 2) (1, 3) (1, 4) (2, 1) (2, 3) (2, 4) (3, 1) (3, 2) (3, 4) (4, 1) (4, 2) (4, 3)
Количество вариантов получится по формуле (n – длина исходной последовательности):
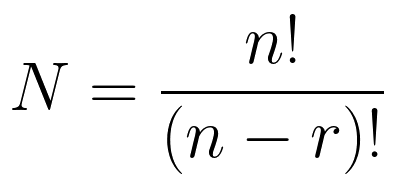
При r > n будет пустое множество, потому что невозможно из более короткой последовательности выбрать более длинную. Максимальное число вариантов – для полной перестановки равняется n! (факториал).
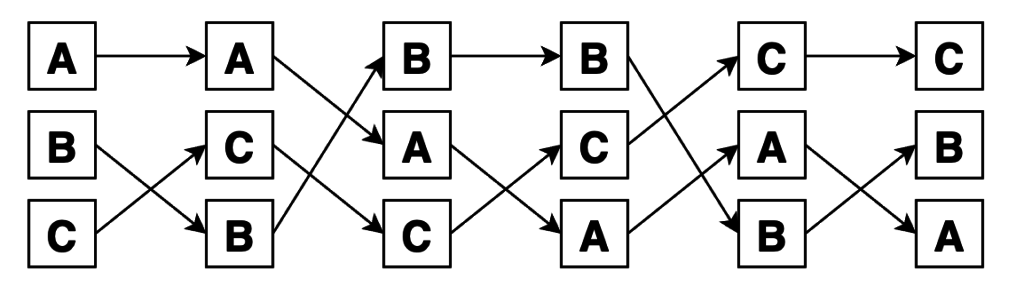
Размещения выглядят так. Сначала выбрали по 2 элемента из 3, а потом переставили их внутри групп всеми способами. Итого 6 вариантов:
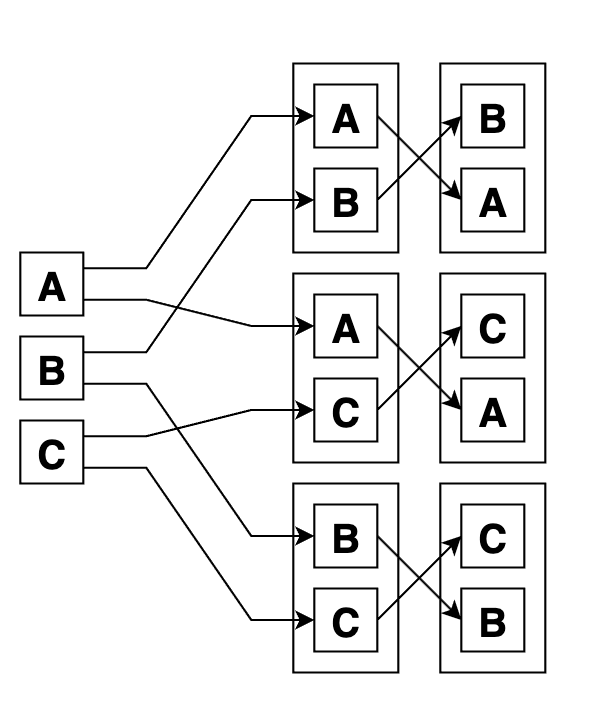
Сочетания
combinations – функция, коротая выбирает все сочетания из входной последовательности. Пусть в ней имеется n различных объектов. Будем выбирать из них r объектов всевозможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по r, а их число равно:
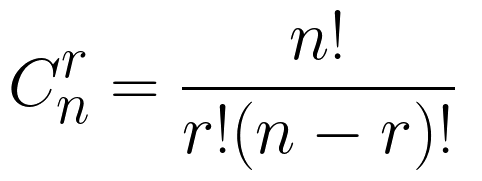
Разница сочетаний и перестановок в том, что для сочетаний нам не важен порядок, а для перестановок он важен. Пример:
>>> print(*permutations([1, 2, 3], 2)) (1, 2) (1, 3) (2, 1) (2, 3) (3, 1) (3, 2) >>> print(*combinations([1, 2, 3], 2)) (1, 2) (1, 3) (2, 3)
(1, 2) и (2, 1) – разные перестановки, но с точки зрения сочетаний – это одно и тоже, поэтому в combinations входит только один вариант из двух.
Второй параметр r – обязателен для этой функции. 0 <= r <= n. При r > n будет пустое множество.
Вот графический пример сочетаний из 3 по 2. Как видно, их вдвое меньше, чем размещений из 3 по 2, так как варианты с перестановками внутри групп не учтены по определению:
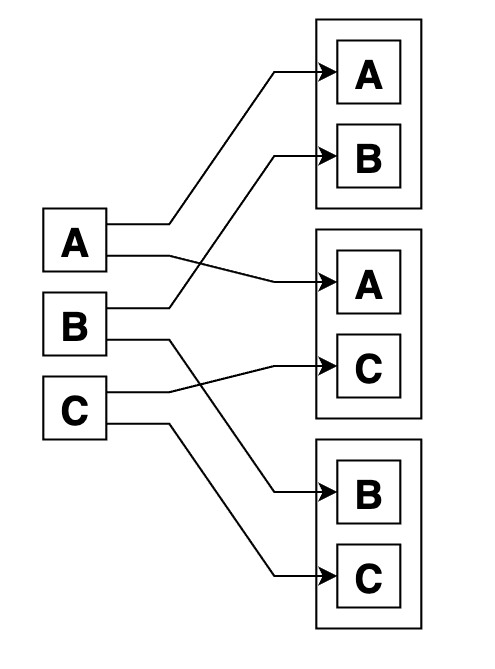
Сочетания с повторами
Функция combinations_with_replacement описывает, сколькими способами можно составить комбинацию по r элементов из элементов n типов (элементы в комбинации могут повторяться, но порядок их не важен). Обратите внимание на слово «тип«, в простых сочетаниях элементы не повторялись внутри одной выборки, они были как бы конкретными экземплярами.
На языке мешка с шарами, сочетания с повторами значит, что мы достаем шары из мешка, а потом кладем их обратно, записывая их цвета (цвет это и есть в данном случае аналог типа). Вполне может быть так, что мы достали красный шар два раза подряд, ведь после первого раза мы сунули его обратно в мешок. Пример:
>>> print(*combinations_with_replacement(['red', 'white', 'black'], 2))
('red', 'red') ('red', 'white') ('red', 'black') ('white', 'white') ('white', 'black') ('black', 'black')
Поэтому, имея возможность брать один и тот же элемент несколько раз, можно выбрать из последовательности в три элемента 4, и 5, и сколь угодно много (больше, чем было исходных типов). Например, по 4 из 2:
>>> print(*combinations_with_replacement(['red', 'black'], 4))
('red', 'red', 'red', 'red') ('red', 'red', 'red', 'black') ('red', 'red', 'black', 'black') ('red', 'black', 'black', 'black') ('black', 'black', 'black', 'black')
Вот графически сочетания с повторами по 2 из 3:
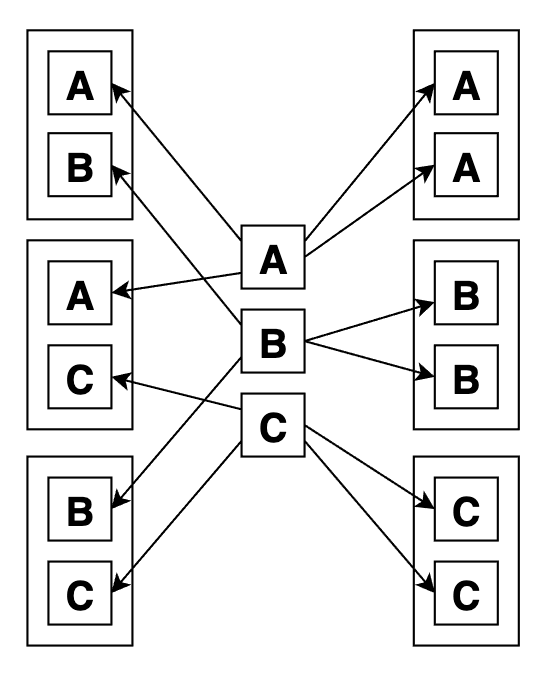
Формула числа элементов на выходе такова:
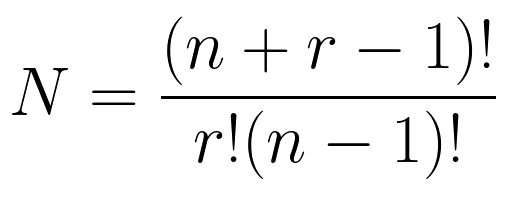
Бонус – брутфорс пароля
Как бонус предлагаю вам применение функции product() для брутфорса паролей. Сперва мы задаем набор символов, которые могут встречаться в пароле, наш алфавит, например такой:
import string # все буквы и цифры alphabet = string.digits + string.ascii_letters # 0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ
А потом перебираем все возможные сочетания с длинами от минимальной до максимальной. Не забываем их склеить в строку:
def brute_force(alphabet, min_len, max_len):
# функция - склеиватель последователностей символов в строку
joiner = ''.join
for cur_len in range(min_len, max_len + 1):
yield from map(joiner, product(alphabet, repeat=cur_len))
Пример применения:
# сокращенный алфавит для иллюстрации работы alphabet = '123AB' print(*brute_force(alphabet, 1, 3), sep=', ') # вывод: 1, 2, 3, A, B, 11, 12, 13, 1A, 1B, 21, 22, 23, 2A, 2B, 31, 32, 33, 3A, 3B, A1, A2, A3, AA, AB, B1, B2, B3, BA, BB, 111, 112, 113, 11A, 11B, 121, 122, 123, 12A, 12B, 131, 132, 133, 13A, 13B, 1A1, 1A2, 1A3, 1AA, 1AB, 1B1, 1B2, 1B3, 1BA, 1BB, 211, 212, 213, 21A, 21B, 221, 222, 223, 22A, 22B, 231, 232, 233, 23A, 23B, 2A1, 2A2, 2A3, 2AA, 2AB, 2B1, 2B2, 2B3, 2BA, 2BB, 311, 312, 313, 31A, 31B, 321, 322, 323, 32A, 32B, 331, 332, 333, 33A, 33B, 3A1, 3A2, 3A3, 3AA, 3AB, 3B1, 3B2, 3B3, 3BA, 3BB, A11, A12, A13, A1A, A1B, A21, A22, A23, A2A, A2B, A31, A32, A33, A3A, A3B, AA1, AA2, AA3, AAA, AAB, AB1, AB2, AB3, ABA, ABB, B11, B12, B13, B1A, B1B, B21, B22, B23, B2A, B2B, B31, B32, B33, B3A, B3B, BA1, BA2, BA3, BAA, BAB, BB1, BB2, BB3, BBA, BBB
Специально для канала @pyway. Подписывайтесь на мой канал в Телеграм @pyway 👈
